1. Bevezető elmélkedések:
Egy táskát helyezek az asztalra.A táska nyugalomban van.
- Hat rá erő? Ha hat rá miért nem gyorsul?
- Mit tudunk a táskára ható erőkről?
- Az inga mozgását milyen erők határozzák meg?
2. Newton harmadik törvénye (hatás-ellenhatás):
A kölcsönhatások során az erők párosával hatnak. Az erő és az ellenerő- azonos nagyságú,
- de ellentétes irányú.
Egy szánkót két ember húz.
Az egyik északi irányba, a másik pedig keleti irányba.
Kérdés:
Merre mozdul el a szánkó?
3. Newton negyedik törvénye:
Az erők egymástól függetlenül, a paralelogramma (vagy a lánc) szabály szerint összegződnek.Paralelogramma szabálynál közös kezdőpontba helyezzük a vektorokat.
Párhuzamosakat húzunk a csúcspontokban (létrejön egy paralelogramma).
A paralelogramma átlója lesz az erők összege/eredője.
Láncszabály esetén: a vektorokat egymás után helyezzük (az első vektor végpontja legyen
a második vektor kezdőpontja.
Az eredő vektor az első vektor kezdőpontjából a második vektor végpontjába mutat.
Következmény:
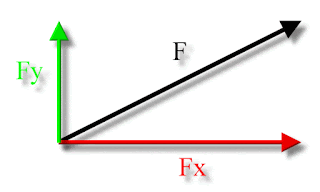
Az erők mindig felbonthatók adott irányú (általában egymásra merőleges) összetevőkre/ komponensekre (esetleg koordinátákra).
Érvényes a Pitagorasz-tétel:
F² = Fx² + Fy²
Mintafeladat:
Fx = 3N
Fy = 4N
F = ?
`F = sqrt(3^2 + 4^2) = 5N`
Alkalmazhatjuk a szögfüggvényeket is:
Fx = F·cos α
Fy = F·sin α
Mintafeladat:
F = 5N
α = 53°
Fx = ?, Fy = ?
Fx = 5·cos53° = 3N
Fy = 5·sin53° = 4N
4. Különféle mozgások dinamikai feltétele:
- Egyenes vonalú egyenletes mozgás:Feredő = 0
- Egyenes vonalú egyenletesen változó mozgás:
Feredő = állandó.
- Szabadesés:
Feredő = Fnehézségi = állandó.
- Egyenletes körmozgás:
Feredő = Fcentripetális (sugárirányú, középpont felé irányuló erő)
- Harmonikus rezgőmozgás:
Feredő = Frugó (nagysága a kitéréssel arányos, de az iránya a kitéréssel ellentétes)
- Ingamozgás: