5. Egyenes vonalú egyenletesen változó mozgás

1. Egyenes vonalú egyenletesen változó mozgás fogalma:

Ha a pályagörbe egyenes, és
a test sebessége egyenlő időközök alatt ugyanannyival változik,
akkor egyenes vonalú egyenletesen változó mozgásról beszélünk.
Az egyenes vonalú egyenletesen változó mozgást végző test gyorsulása állandó.

2. Jellemzője:

gyorsulás = sebesség változási gyorsasága
jele: a (akceleráció)
képlete:
    `a = (Δv)/(Δt)` (általános esetben)

   (1.A.) `color(red)(a = v/t)`
   (1.B.) `v = a*t`
   (1.C.) `t = v/a`

mértékegysége:
    `m/s^2`

3. Grafikonok, további képletek:

gyorsulás-idő grafikon

A grafikon alatti terület a sebességet adja.

sebesség-idő grafikon:

A grafikon alatti terület egyenlő a megtett úttal.
Képletek:

   (2.) `color(red)(s = (v*t)/2)`

    `v = a*t` helyettesítéssel:

    (3.) `color(red)(s = 1/2*a*t^2)` (négyzetes út törvény).

    `t = v/a` helyettesítéssel:

    (4.) ` color(red)(s = v^2/(2*a))`.

út-idő grafikon:

A grafikon képe: parabola.

4. Szabadesés esetén:

`a = g = 9,81m/s^2` (nehézségi gyorsulás)
Képletek:
      g = v/t
      v = g*t
    t = v/g
    `s = 1/2*g*t^2`
   ` s = v^2/(2*g)`

5. Kezdősebességgel rendelkező eset:

Grafikonok:
gyorsuló mozgás esetén:

lassuló mozgás esetén:

Igaz-hamis állítások

NÉV: PONT:
Igaz-hamis állítások:

Ssz.	Állítás	Igaz	Hamis	?
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

4. Egyenes vonalú egyenletes mozgásra vonatkozó számolásos feladatok

1. Átlagsebesség-számításra vonatkozó alapfeladatok

(Szakaszonként egyenes vonalú egyenletes mozgás esetén)

MINTAFELADATOK

1. Egy test 100 m utat tesz meg 30 s alatt, majd 200 m utat 50 s alatt.
Mekkora az egész útra számított átlagsebessége?
Adatok:
`s_1 = 100m`
`t_1 = 30s`
`s_2 = 200m`
`t_2 = 50s`

`s_(össz) = s_1 + s_2 = 100m + 200m = 300m`
`t_(össz) = t_1 + t_2 = 30s + 50s = 80s`
`v_(átl) = s_(össz)/t_(össz) = (300m)/(80s) = 3,75m/s `

1. Képlet:
`color(red)(v_á = (s_1 + s_2)/(t_1 + t_2))`

2. Egy test 3s-ig haladt 20m/s sebességgel, majd 2s-ig 30m/s sebességgel.
Mekkora az egész útra számított átlagsebessége?
Adatok:
`v_1 = 20m/s`
`t_1 = 3s`
`v_2 = 30m/s`
`t_2 = 2s`

`s_1 = v_1*t_1 = 20*3 = 60m`
`s_2 = v_2*t2 = 30*2 = 60m`
`s_(össz) = s_1 + s_2 = 60 + 60 = 120m`
`t_(össz) = 3 + 2 = 5s`
`v_(átl) = s_(össz)/t_(össz) = 120/5 = 24m/s`

2. Képlet:
`color(red)(v_á = (v_1*t_1 + v_2*t_2)/(t_1 + t_2))`
Ha t = t₁ = t₂, akkor
`color(blue)(v_á = (v_1*t + v_2*t)/(t + t) = (v_1 + v_2)/2)`
Vagyis, ha az időtartalmak hossza egyenlő, akkor az átlagsebesség a sebességek számtani átlagával egyenlő.

3. Egy test 50 m utat tesz meg 2 m/s sebességgel, majd 30 m utat 3 m/s sebességgel.
Mekkora az egész útra számított átlagsebessége?
Adatok:
`v_1 = 2m/s`
`s_1 = 50m`
`v_2 = 3m/s`
`s_2 = 30m`

`t_1 = s_1/v_1 = 50/2 = 25s`
`t_2 = s_2/v_2 = 30/3 = 10s`
`s_(össz) = s_1 + s_2 = 50 + 30 = 80m`
`t_(össz) = t_1 + t_2 = 25 + 10 = 35s`
`v_(átl) = s_(össz)/t_(össz) = 80/35 = 2,2857m/s`

3. Képlet:
`color(red)(v_á = (s_1 + s_2)/(s_1/v_1 + s_2/v_2))`
Ha s = s₁ = s₂, akkor
`color(blue)(v_á = (s + s)/(s/v_1 + s/v_2)= 1/((1/v_1+1/v_2)/2) = (2*v_1*v_2)/(v_1+v_2))`
Vagyis, ha az uthosszak egyenlők, akkor az átlagsebesség a sebességek harmonikus átlagával egyenlő.
Harmonikus átlag reciproka = adatok reciprokának számtani átlaga.

---

Gyakorló feladatok:

1. Feladat:
`s_1 = 25 km`
`t_1 = 0,5 h`
`s_2 = 75 km`
`t_2 = 1,25 h`
`v_(átlag) = ?`

2. Feladat:
`v_1 = 55 (km)/h`
`t_1 = 0,8 h`
`v_2 = 75 (km)/h`
`t_2 = 0,6 h`
`v_(átlag) = ?`

3. Feladat:
`v_1 = 35 (km)/h`
`s_1 = 0,8 km`
`v_2 = 45 (km)/h`
`s_2 = 1,2 km`
`v_(átlag) = ?`

4. Egy vonat a 20km-es távolság első felét 20km/h, a második felét 30km/h sebességgel teszi meg.
Mekkora az átlagsebessége?

5. Egy gépkocsi 10 percig ment 30km/h, majd ugyanannyi ideig 40km/h sebességgel.
Mekkora az átlagsebessége?

6. Egy gépkocsinak a 3 órás útja során 40km/h volt az átlagsebessége.
Fél óráig 34km/h, majd x ideig 50km/h, majd kétszer ennyi ideig 20km/h volt a sebessége.
Mekkora az x értéke?

---

2. Grafikonelemzéses feladatok

1. Elemezzük a következő elmozdulás-idő grafikont!

Az elmozdulás annyiban tér el az úttól, hogy előjeles mennyiség, vagyis az mozgás irányát is megmutatja.

A mozgás 3 szakaszra bontható:
1. szakasz: odaút (a test folyamatosan távolodik)
2. szakasz: a test nem mozog (áll)
3. szakasz: visszaút (a test folyamatosan közeledik)

Határozzuk meg a mozgás jellemzőit:
`s_1 = ?`
`t_1 = ?`
`v_1 = ?`

`s_2 = ?`
`t_2 = ?`
`v_2 = ?`

`s_3 = ?`
`t_3 = ?`
`v_3 = ?`

`v_(átlag) = s_(összes)/t_(összes)`
`v_(átlag) = (|s_1| + |s_2| + |s_3|)/(t_1 + t_2 + t_3)`

A) Készítsük el a mozgás út-idő grafikonját!

Megoldás:

B) Készítsük el a mozgás sebesség-idő grafikonját!

 Megoldás:

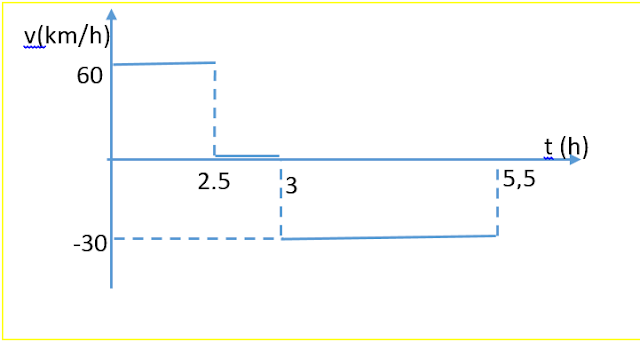
 2. Adott egy mozgás sebesség-idő grafikonja. Határozzuk meg a mozgás út-idő és elmozdulás-idő grafikonját!

Gyakorló feladatok:
1.

 2.

 3.

 4.

3. Egyenes vonalú egyenletes mozgás

1. Mikor beszélünk egyenes vonalú egyenletes mozgásról?

 Ha a pályagörbe alakja egyenes, és
a test azonos időközönként azonos utakat tesz meg,
akkor egyenes vonalú egyenletes mozgásról beszélünk.

Ez egyenes vonalú egyenletes mozgást végző testnek a sebessége állandó.

• pl. légpárnás asztalon mozgó kiskocsi,
• jégen csúszó korong,
• világűrben magára hagyott test,
• Mikola-csőben a buborék

2. Mi a legfőbb jellemzője az egyenes vonalú egyenletes mozgásnak?

 sebesség = megtett út és az út megtételéhez szükséges idő hányadosa.
jele: v (velocitas)
képlete:
    v = Δs/Δt (általános esetben)
    v = s/t
    s = v*t
    t = s/v
mértékegysége:
    m/s
átváltás:
    1m/s = 3,6km/h

Feladatsorokban szereplő fontosabb sebességértékek:

1. gyalogos:                      5 km/h

2. kerékpáros:                  15 km/h

3. autó:                             100 km/h

4. hang (levegőben):         340 m/s

5. fény (levegőben):         300 000 km/s

3. Feladatok:

1.     25 m/s = ? km/h

2.     40 km/h = ? m/s

3.     s = 250 m
        t = 8 s
        v = ?

4.     v = 3,5 m/s
        t = 12 s
        s = ?

5.     s = 300 m
        v = 4 m/s
        t = ?

4. Ábrázoljuk a megtett utat és a sebességet az idő függvényében!

út-idő grafikon:

Az út-idő grafikon meredeksége a sebességet adja.

sebesség-idő grafikon:

A sebesség-idő grafikon alakja (az időtengellyel párhuzamos) vízszintes egyenes.
A sebesség-idő grafikon alatti terület a megtett úttal egyenlő.

5. Átlagsebesség számítás

Ha két útszakaszon különböző sebességekkel megyünk, akkor mekkora állandó sebességgel kellene mennünk, hogy ugyanannyi összidő alatt ugyanannyi össz utat tegyünk meg?
átlag sebesség = összes megtett útnak és az összes időnek a hányadosa
      `v_(átl) = s_(össz)/t_(össz)`
ahol
     ` s_(össz) = s_1 + s_2`
     ` t_(össz) = t_1 + t_2`

Igaz-hamis állítások

NÉV: PONT:
Igaz-hamis állítások:

Ssz.	Állítás	Igaz	Hamis	?
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

2. Mozgástani alapfogalmak

1. Melyik részénél tartunk a fizikának?

   Kinematika =
      a pontszerű testek mozgásainak matematikai leírásával foglalkozik.

2. Minek a milyét vizsgáljuk?

   Pontszerű test/ tömegpont =
    olyan test, amelynek a mérete elhanyagolható a pályagörbe hosszához képest.
    ez a lehető legegyszerűbb testmodell.
      pl. egy mozgó repülőgép

   Mozgás =
    a pontszerű test helyének változása

   Nyugalom/ nyugalmi állapot =
    a pontszerű test helyének változatlansága

Stroboszkóp = azonos időközönként készít pillanatfelvételeket, majd ezeket egymásra illeszti.
pl.

3. Mihez képest vizsgáljuk a tömegpont mozgását?

   Vonatkoztatási pont =
    az a rögzített helyzetű pont, amelyhez viszonyítva vizsgáljuk a test mozgását.
   Vonatkoztatási rendszer =
    az a koordináta rendszer, amelynek a kezdőpontja a vonatkoztatási pont.

4. Milyen fizikai mennyiségekkel jellemezhetjük egy test mozgása?

   Pályagörbe =
    olyan pontokból áll, amelyen a test áthalad a mozgása során.

   Megtett út =
    a pályagörbe hossza
    jele:
      s (spatium = spácium)
      Δs = delta es = az es változása
    mértékegysége: m (méter)

  Idő =
      az út megtételéhez szükséges időtartam
    jele:
      t (tempora)
      Δt = delta té = a té változása
    mértékegysége:
      s (szekundum = másodperc)

5. Milyen mozgásformákat ismerünk?

   A pályagörbe alakja alapján a mozgás lehet

•  egyenes vonalú mozgás = a pályagörbe egy egyenes,
•  körmozgás = a pályagörbe alakja kör,
•  bolygómozgás = a pályagörbe alakja ellipszis.

Igaz-hamis állítások

NÉV:
Azonosító:
PONT:
Igaz-hamis állítások:

Ssz.	Állítás	Igaz	Hamis	?
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

1. A 9. Fizika témakörei

1. A mechanika fogalma

Mechanika = a fizika azon része, amelyik a mozgásokkal foglalkozik

2. A mechanika részei

1. Pontszerű testek vizsgálata:

• Kinematika = a mozgások matematikai leírása
• Dinamika = a mozgások magyarázata
• Munka, energia, teljesítmény, hatásfok

2. Pontrendszerek vizsgálata

3. Merev testek  vizsgálata

• Merev egyensúlya (Sztatika)

4. Deformálható testek vizsgálata

• Rugalmasságtan (Szilárdságtan)
• Folyadékok és gázok fizikája
• Rezgések, hullámok, hangtan